Soit \(f:I\to\Bbb R\), avec \(I\) un intervalle de \(\Bbb R\)
Définition : on dit que \(f\) est continue en un point \(x_0\in I\) si $$\forall\epsilon\gt 0,\exists\delta\gt 0,\forall x\in I,|x-x_0|\lt \delta\Rightarrow|f(x)-f(x_0)|\lt \epsilon$$
Autrement dit si \(\underset{x\to x_0}\lim f(x)=f(x_0)\)
Soit \(f:I\to\Bbb R\) et \(x_0\in I\). Si \(f\) est continue en \(x_0\) et si \(f(x_0)\neq 0\), alors \(\exists\delta\gt 0\) tel que $$\forall x\in]x_0-\delta,x_0+\delta[, f(x)\neq0$$
Démonstration :
Par la définition de continuité en \(x_0\), $$\forall\epsilon\gt 0,\exists\delta\gt 0\text{ tq }\forall x\in ]x_0-\delta,x_0+\delta[\Rightarrow f(x_0)-\epsilon\lt f(x)\lt f(x_0)+\epsilon$$
On choisit \(\epsilon\) tq \(0\lt \epsilon\lt f(x_0)\)
Il existe alors un intervalle \(J=I\cap]x_0-\delta,x_0+\delta[\) tq \(\forall x\in J,f(x)\gt 0\)
Idem pour \(f(x)\lt 0\)
Corollaire :
Soit \(f:]a,b[\to\Bbb R\) est continue en \(x_0\in]a,b[\) si et seulement si $${{\begin{cases}\forall(u_n)_{n\in\Bbb N},u_n\underset{n\to+\infty}\longrightarrow x_0\\ u_n\in]a,b[,n\geqslant1\end{cases} }}\implies {{f(u_n)\underset{n\to+\infty}\longrightarrow f(x_0)}}$$
(Limite)
Définition :
La fonction \(f:E\subset{\Bbb R}^n\to{\Bbb R}\) est continue en \(x_0\in E\) si $$\displaystyle{\lim_{x\to x_0} } f(x)=f(x_0)$$
On dit que \(f\) est continue sur \(I\) si \(f\) est continue en tout point de \(I\)
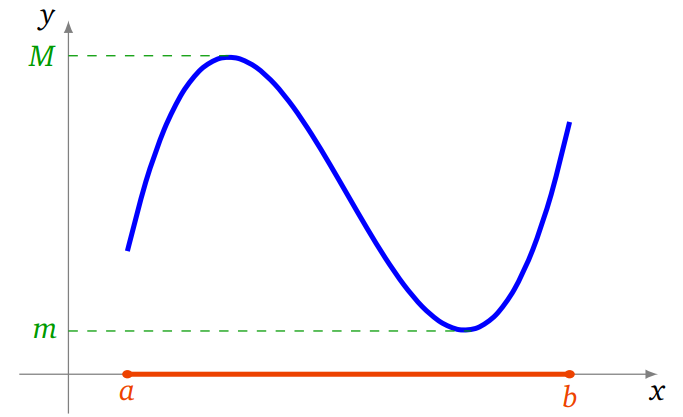
Intuitivement, une fonction est continue si on peut tracer son graphe sans lever la main
Prolongement par continuité
Théorème des valeurs intermédiaires
Théorème des valeurs extrêmes
Théorème de la bijection
Soient \(f,g:I\to\Bbb R\) continues en \(x_0\in I\)
Alors
- \(\lambda f\) est contine en \(x_0\)
- \(f+g\) est continue en \(x_0\)
- \(f\times g\) est continue en \(x_0\)
- Si \(f(x_0)\neq 0\), alors \(\frac1f\) est continue en \(x_0\)
Pour voir si une fonction du type \(f(x)=\begin{cases}f(x),x\lt x_0\\ g(x), x\geqslant x_0\end{cases}\) est continue (avec \(f\) et \(g\) continues), on regarde si \(\underset{x\lt x_0}{\underset{x\to x_0}\lim}f(x)=g(x_0)\)